سه تایی فیثاغورسی

هر سه تایی به صورت (a,b,c) را که تشکیل رابطه فیثا غورس (c²=a²+b²)در مثلث قائم الزاویه را بدهند به سه تایی های فیثا غورثی معروفند .

برای تشکیل و بدست آوردن سه تایی های فیثا غورسی می توان با جایگذاری  به جای u و v  مقادیری برای a و b و c بدست آورد .

 a=2uv

b=u²-v²

c=u²+v²

( به شرط اینکه اولا u  و v  با هم برابر نبوده

و دوم نسبت به هم اول باشند  1= (u,v)

و سوم اینکه   u>v  باشد   )

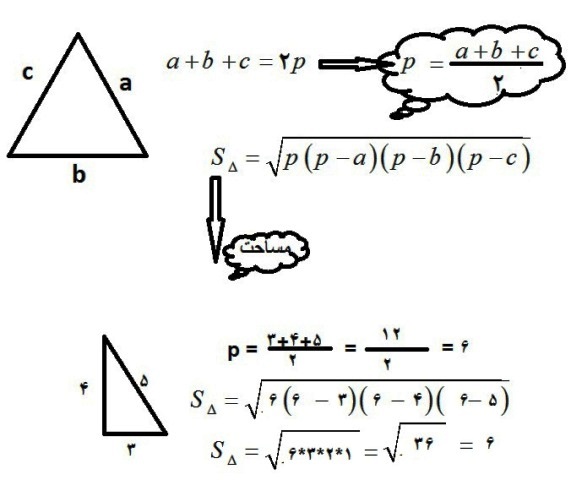
به عنوان مثال اگر به u=2 و v=1 بدهیم مقادیر a=4 و b=3 و c=5 را به ما می دهد که با می دانیم با توجه به رابطه  فیثاغورس تشکیل یک مثلث قایم الزاویه را می دهد .

3²+4²=5²

16+9=25

حدس های گلدباخ

گلد باخ رياضي دان آلماني بود كه در سال 1750 در روسيه زندگي ميكرد.

حدس او در مورد اعداد زوج:

هر عدد زوج بالاتر از 4 حاصل جمع دو عدد اول است

48=11+37.......18=11+7.......20=17+3....

حدس او در مورد اعداد فرد:

هر عدد فرد بزرگتر از 5 را ميتوان به صورت حاصل جمع سه عدد اول نوشت.

9=2+2+5.....13=3+3+7.......

این پزشک متوجه حقیقت جالبی شده بود و آن هم این بود که هر عدد زوج را می توان به صورت مجموع دو عدد اول نوشت. (البته عدد یک را به این خاطر از مجموعه اعداد اول کنار گذاشتند که صورت مسئله های نظریه اعداد کوتاه تر شود. زیرا اگر این کار را نمی کردند بایستی در اکثر صورت مسئله های مربوط به اعداد اول می نوشتند: "به غیر از یک") اکنون به دلیل همین موضوع عدد 2 از حدس گلدباخ خارج شده است. 

از عجايب رياضي

13837x your age x 73 

and see what's happen

 

سیزده هزار و هشتصد و سی و هفت ضربدر سن شما ضربدر هفتاد و سه

 امتحان کنید ضرر نداره

 

 

 

  

سن شما و سن شما و سن شما=x73سن شما13837x

 

رابطه ریاضی 11

9=۲۱-۱۲  و    9=23-32    و    9=34-43   و........

اگر رقم­های عدد داده شده یک واحد از هم فاصله داشته باشند، اختلاف آن­ها همیشه 9 می­شود. که می­توان از رابطه­ی   9=9×1 نیز آن را به دست آورد.

 

           18=۴۲-۲۴  و    18=35-53   و  18=۴6-6۴ و....

اگر رقم­های عدد داده شده دو واحد از هم فاصله داشته باشند، اختلاف آن­ها همیشه 18 می­شود. که می­توان از رابطه­ی   18=9×2 نیز آن را به دست آورد.

 

          27=۴۱-۱۴  و    27=25-52   و   27=36-63 و......

 

اگر رقم­های عدد داده شده سه واحد از هم فاصله داشته باشند، اختلاف آن­ها همیشه ۲۷ می­شود. که می­توان از رابطه­ی   27=9×3 نیز آن را به دست آورد.

و.....

               72=۹۱-۱۹

که چون 9 و 1، هشت واحد اختلاف دارند اختلاف 19 و 91 شده ۷۲:    ۷۲=9×8

شگفتیهای اعداد

63 ÷ 3=6 ×3+3

95÷5=9+5+5

85-63=8+5+6+3

272+16=(2+7) ×2  ×16

√64=6+√4

√6724=6+72+4

√169=√16+9

√11881=118-8-1

---

منبع : http://math-sch.blogfa.com/

کوتاه و خواندنی

چند سال سن دارید : سن خودرا به ماشین حساب بدهید سپس آنرا در 7 ضرب کنید حاصلضرب را نیز در 1443 ضربنمایید با کمال تعجب خواهید دید سن شما سه بار تکرار شده است (برگرفته از کتاب سرگرمیهای ریاضی)

اطلاعاتی راجع به خواندن اعداد بزرگ

هزار  (thousand ) = 10³

میلیون (  million) = 10⁶

میلیارد  ( milliard) = 10⁹

بیلیون  (  billion) = 10¹²

تریلیون (  trillion) = 10¹⁵

کوادریلیون (quadrillion) = 10¹⁸

کوئینتیلیون (quintillion) = 10²¹

سیکستیلیون (sixtillion) = 10²⁴

سپتیلیون (septillion) = 10²⁷

اکتیلیون (octillion) = 10³⁰

نونیلیون (nonillion) = 10³³

دسیلیون (decillion) = 10³⁶

دسیلیون ( decillion) = 10³⁶

آن دسیلیون ( Undecillion) = 10³⁹

دو دسیلیون ( Dodecillion) = 10⁴² 
تری دسیلیون ( Tredecillion) = 10⁴⁵ 
کواتر دسیلیون ( Quattordecillion) = 10⁴⁸ 
کوئین دسیلیون ( Quindecillion) = 10⁵¹ 
سیکس دسیلیون ( Sixdecillion) = 10⁵⁴ 
سپتن دسیلیون ( Septendecillion) = 10⁵⁷ 
اکتو دسیلیون ( Octodecillion) = 10⁶⁰ 
نووم دسیلیون ( Novemdecillion) = 10⁶³ 
ویجینتیلیون ( Vigintillion) = 10⁶⁹ 
آن ویجینتیلیون ( Unviigintillion) = 10⁷² 
دو ویجینتیلیون ( Doviigintillion) = 10⁷⁵ 
تری ویجینتیلیون ( Treviigintillion) = 10⁷⁸ 
کواتر ویجینتیلیون ( Quattorviigintillion) = 10⁸¹ 
کوئین ویجینتیلیون ( Quinviigintillion) = 10⁸⁴ 
سیکس ویجینتیلیون ( Sixviigintillion) = 10⁸⁷ 
سپتن ویجینتیلیون ( Septenviigintillion) = 10⁹⁰ 
اکتو ویجینتیلیون ( Octoviigintillion) = 10⁹³ 
نووم ویجینتیلیون ( Novemviigintillion) = 10⁹⁶

بدست آوردن مساحت هر مثلث با دانستن مقدار هر 3 ضلع

می دانیم که مساحت مثلث در حالت کلی برابر       2/ (ارتفاع*قاعده)

در این روش ، فرمولی ارائه می شود که شما را  قادر  می سازد مساحت هر نوع مثلثی را با دانستن مقدار 3 ضلع آن محاسبه کنید .

فرض کنیم a و b و  c  اضلاع مثلث باشند و داشته باشیم :

یك خاصیت جالب عدد 9

عدد 9 به خصوص برای بچه هایی كه جدول ضرب را به سختی یاد می گیرند عدد بسیار جالبی است:زیرا می شود از بخاطر سپردن حاصلضربها در 9 صرفنظر كرد .برای چه به حافظه خود فشار أوریم؟ وجود ده انگشت كافی است. برای این منظور باید هر دو دست را باز كرد سپس از سمت چپ شماره انگشتی را كه میخواهیم در 9 ضرب كنیم خوابانده :حاصلضرب أن عدد در9 بطور عملی نشان داده می شود.

مثلا اگر بخواهیم 9 را در 3 ضرب كنیم انگشت سوم را از سمت چپ خوابانده و حاصلضرب را میخوانیم.

رابطه های جالب 11

عدد 2520 را می‌توان بر اعداد 1 تا 10 تقسیم نمود، بدون آن‌که خارج قسمت کسری داشته باشد.

و جالب تر اینکه این عدد کوچکترین عددی است که بر همه این اعداد (1 .. 10 ) بخش پذیر است .

و باز هم جالب تر از آن اینست که بدانیم این عدد از حاصلضرب چه عواملی ایجاد می شود ؟

2520=12*30*7

که اعدادی خاص هستند ...    7 ==>   هفت روز هفته

                                          30==>   سی روز ماه

                                          12==>   دوازده ماه سال

و نکته ریاضی جالب آن اینست که اگر این عوامل را تجزیه کنیم و عوامل اول آن را بیابیم .. همان اعداد 1 تا 10 هم بدست می آیند ..

رابطه های جالب 10

یکی از  رابطه های جالب ریاضی این است‌ که :

وقتی عدد 111111111 را در خودش ضرب کنی،

جواب خواهد شد؛

12345678987654321

---

=111111111*111111111

12345678987654321

بدست اوردن مربع کلیه اعداد با یکان 5

فرض کنید عدد به صورت زیر باشد:
ab5
aصدگان
bدهگان
یکان5
حاصل مربع این عدد به شکل زیر میباشد:
دورقم سمت راست:25
سایر ارقام سمت چپ:
ab+1*ab

مثال:
مربع 75:
دو رقم سمت چپ:25
سایر ارقام سمت راست:
7*(7+1)=56
جواب مربع 75 :5625
مثالهای بیشتر:

مربع195=38025
مربع1995=398025
مربع245=60025

__________________

محاسبه ای جالب

                                

  1 x 9 + 2 = 11 

 12 x 9 + 3 = 111 

 123x9+4 = 1111

 1234 x 9 + 5 = 11111

 12345 x 9 + 6 = 111111

 123456 x 9 + 7 = 1111111

 1234567 x 9 + 8 = 11111111

 12345678 x 9 + 9 = 111111111

 123456789 x 9 +10= 1111111111        

یک رابطه جدید ریاضی

ضربهای جالب

رابطه های جالب 9